题目描述
根据二叉树的前序遍历和中序遍历的结果,重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
1 | preorder = [3,9,20,15,7] |
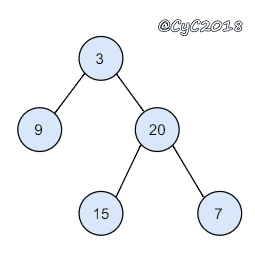
思路
前序遍历的第一个值为根节点的值,使用这个值将中序遍历结果分成两部分,左部分为树的左子树中序遍历结果,右部分为树的右子树中序遍历的结果。
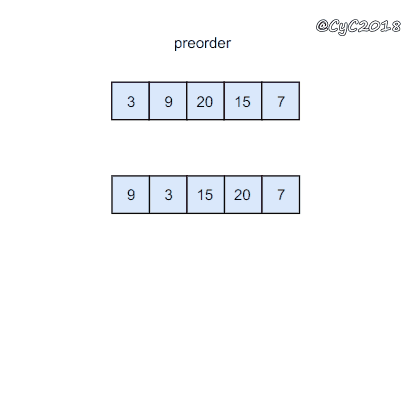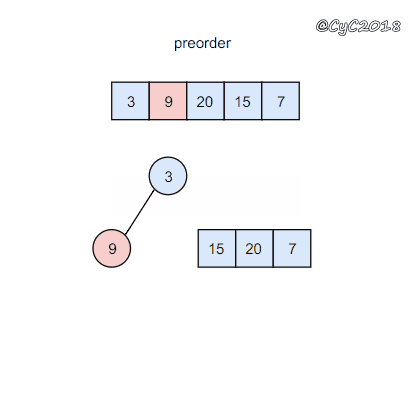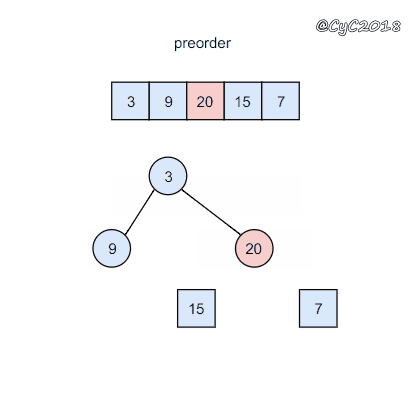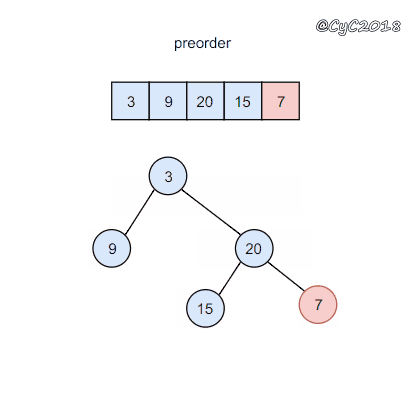
1 | //二叉树结构 |
拓展
重建一棵二叉树:
前序+中序
后序+中序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29//二叉树结构
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(int val){this.val = val; left = null; right = null};
}
//缓存中序遍历数组每个值对应的索引
public Map<Integer, Integer> indexForInOrder = new HashMap<>();
public TreeNode reConstructBinaryTree(int[] next, int[] in){
for(int i=0; i<in.length; i++){
indexForInOrder.put(in[i], i);
}
return reConstructBianryTree(next, next.length-1, 0, 0);
}
//参数:后序遍历数组、后序部分数组右边界,后序部分数组左边界、中序部分数组左边界
private TreeNode reConstructBinaryTree(int[] next, int nextR, int nextL, int inL){
if(nextL > nextR)
return null;
TreeNode root = new TreeNode(next[nextR]);
int rightTreeSize = indexForInOrder(root.val) - inL;
//对于nextR和nextL的计算:LRD
//对于inL的计算:LDR
root.right = reConstructBinaryTree(next, nextR-1, nextR-rightTreeSize, inL);//L(R)D
root.left = reConstructBinaryTree(pre, nextR-rightTreeSize-1, nextL, inL+leftTreeSize+1);//(L)RD
return root;
}
